CRYOLOGIE - Cryophysique

CRYOLOGIE - Cryophysique

La température est l’un des facteurs les plus importants en physique, mais le milieu terrestre n’en offre qu’une ambiance aux limites restreintes. Dès la seconde moitié du XX^e siècle, après avoir dépassé le stade de la liquéfaction de tous les gaz, y compris celui de l’hélium (face=F0019 漣 268,93 ⁰C ou 4,22 K), réalisée dès 1908 à Leyde par le physicien néerlandais Kamerlingh Onnes (1853-1926), on s’est efforcé à produire des froids de plus en plus intenses. Les connaissances, en particulier dans le domaine de la physique des solides, s’en sont trouvées considérablement accrues et, au cours des recherches, se sont manifestés des phénomènes inattendus comme la supraconductivité et la superfluidité de l’hélium. Débordant le cadre du laboratoire, l’étude des grands froids s’impose dans la technique industrielle. D’après l’usage courant du laboratoire, on entend par cryophysique le domaine des températures inférieures à celle de l’hydrogène liquide à la pression barométrique normale (face=F0019 漣 253 ⁰C), tandis que d’après la coutume de l’industrie on l’étend généralement jusqu’à la température correspondante de l’air liquide (face=F0019 漣 190 ⁰C).

Le présent chapitre relève de la première définition car elle correspond plus fidèlement aux diverses manifestations macroscopiques de la physique quantique qui, en raison de son formalisme particulier, nécessite un traitement séparé justifiant l’adoption d’une dénomination distincte.

En revanche, dans ce qui suit, les titres de cryologie et de cryogénie doivent être entendus dans l’acception plus large de leur signification étymologique. Ils couvrent dès lors tout le domaine des températures inférieures à 0 ⁰C, ce qui permet d’y inclure les méthodes de réfrigération à tous les niveaux.

1. Aspects fondamentaux

Intérêt des basses températures

La signification de la grandeur «température» est examinée dans les articles THERMODYNAMIQUE, mécanique STATISTIQUE et thermodynamique STATISTIQUE. À une augmentation de la température T correspond en général une augmentation du désordre d’un système en équilibre. Par exemple, sous l’effet de l’agitation thermique, les atomes d’un solide subissent, autour d’une position moyenne, des mouvements désordonnés de vitesse et d’amplitude de plus en plus grandes.

On peut donner une forme plus théorique aux remarques précédentes. Un système physique quelconque peut se trouver dans des niveaux (ou états) d’énergie E ⁱ différents. Le plus bas de ces niveaux d’énergie, E ⁰, s’appelle le niveau fondamental . Les autres sont appelés niveaux excités . Lorsque les niveaux sont très voisins, on note dn = g (E )dE leur nombre compris entre E et E + dE ; la fonction g (E ) caractérise la distribution des niveaux du système; on l’appelle densité des états , et sa connaissance est indispensable. Elle est en général de plus en plus compliquée à mesure que E croît.

À la température T , le système peut se trouver dans l’un quelconque des états E ⁱ , mais avec une probabilité proportionnelle au facteur de Boltzmann e ^{–E i /kT} . Il «saute» très rapidement d’un état à un autre, son énergie varie, et l’on peut seulement mesurer son énergie moyenne E 漣:

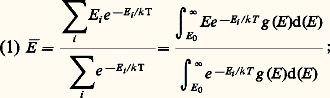le dénominateur exprime simplement que la somme des probabilités est égale à 1; k est la constante de Boltzmann, qui vaut 1,38 憐 10^-23 J . K^-1.

À 0 K (kelvin), le système est dans le niveau fondamental. À mesure que T croît, les états proches du fondamental ont une probabilité croissante d’être réalisés. Les mesures à basses températures donnent donc des informations sur les niveaux faiblement excités. Dans certaines conditions, on peut également étudier la rapidité avec laquelle le système passe d’un état à un autre et connaître ce qu’on appelle la durée de vie d’un état. Ces changements sont à l’origine des phénomènes de bruits thermiques, dont le plus connu est le bruit Nyquist, caractérisé par l’apparition d’un potentiel fluctuant V (T ), dû à l’agitation des électrons, aux bornes d’une résistance R , tel que dans une bande de fréquence f :

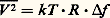Une autre façon de décrire ces résultats consiste à associer à l’augmentation d’énergie à partir du fondamental, des excitations fictives qu’on appelle des «quasi-particules» et qui sont, d’après les lois de la mécanique quantique, des quanta d’énergie. Par exemple, à l’augmentation d’énergie mécanique due à l’agitation thermique des atomes d’un solide, on associe des quanta d’énergie appelés phonons . On peut aussi introduire des quanta associés au désordre de l’aimantation: on les appelle alors magnons ; on connaît également les polarons , les plasmons , etc. Toutes ces quasi-particules se comportent, au point de vue théorique, comme des particules réelles: atomes d’un gaz, électrons, etc. Aux basses températures, le gaz fictif des quasi-particules d’un système est raréfié, puisque le système est peu excité; les interactions possibles entre ces quasi-particules sont alors peu importantes du fait de leur raréfaction: on a la possibilité d’analyser simplement et d’une façon féconde les propriétés du système.

Chaque branche de la physique, en particulier la physique du solide, se prolongeant dans le domaine des basses températures (fig. 1), il n’est pas possible d’en faire un examen complet; on se bornera aux notions les plus importantes.

Capacités calorifiques des solides

Elles sont étroitement liées à la densité des états. L’énergie moyenne E 漣⁰, donnée dans la formule (1), est identique à l’énergie interne U définie à l’article THERMODYNAMIQUE sous la notation E . La capacité calorifique C ^R est égale au rapport U / T de l’augmentation U d’énergie à fournir au corps pour élever sa température de T . On mesure en général C à la pression barométrique normale mais, aux basses températures, cette valeur est très peu différente de celle qu’on obtiendrait à volume constant et une telle distinction n’est pas nécessaire. U et C ont différentes origines selon que le solide contient ou non des électrons de conduction, qu’il est magnétique ou pas, etc. On examinera successivement certaines contributions.

L’agitation thermique des atomes, ou capacité calorifique de réseau, C ^R, existe dans tous les solides; c’est la seule capacité calorifique qu’on trouve dans les corps isolants et non magnétiques. Expérimentalement, on trouve que C tend vers zéro à basse température, suivant une loi en T ³. La théorie a été établie par Debye; elle est fondée sur les analogies entre le gaz de phonons et le gaz des photons du rayonnement électromagnétique (théorie du rayonnement). Le coefficient de proportionnalité de la loi en T ³ varie d’une substance à l’autre; on l’exprime à l’aide d’un paramètre , appelé température de Debye, qui est caractéristique de la substance (tabl. 1). Ainsi pour une mole d’un corps solide:

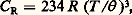R : constante des gaz = 8,32 J . K^-1. est proportionnel à la vitesse moyenne du son dans le solide.

La loi en T ³ est valable jusqu’à T 麗 /10; toutefois le paramètre n’est pas rigoureusement constant; si T 礪 , C ^R tend vers 3 R (loi de Dulong et Petit). La notation utilisée plus loin pour l’échelle Celsius ne devrait pas prêter à confusion.

On ne trouve les électrons libres en nombre appréciable que dans les métaux et semi-métaux. Les électrons ont des densités d’état très variables d’un corps à l’autre; c’est ce qui donne un intérêt à la mesure de la capacité calorifique électronique C ^e. Ces particules obéissent à la statistique de Fermi-Dirac; C ^e varie linéairement avec T selon la loi:

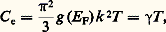où g (E ^F) est la densité des états électroniques à la surface de Fermi. Dans un métal, les chaleurs électroniques et de réseau coexistent; on les distingue grâce à la différence de leur variation avec T . La capacité calorifique totale est:

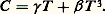Le rapport C ^e/C ^R varie en 1/T ²: la chaleur spécifique électronique devient prédominante aux basses températures; en pratique, c’est dans la région de l’hélium liquide qu’on parvient à la mesurer (tabl. 2).

Une valeur élevée de 塚 est un signe de forte densité électronique et est caractéristique des métaux dits de transition (tabl. 2).

Dans les substances magnétiquement ordonnées, les magnons sont assez analogues aux phonons; les densités d’état diffèrent selon que la substance est ferromagnétique (C ^M 黎 T ^3/2) ou antiferromagnétique (C^M 黎 T ³).

Les anomalies de Schottky se rencontrent en général chaque fois que le nombre de niveaux est fini. Le cas le plus simple correspond à deux niveaux:

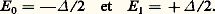On trouve avec la formule (1) que:

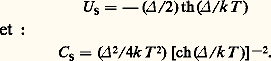La partie à droite du maximum, appelée queue de l’anomalie de Schottky, varie en 1/T ² (fig. 2). Il est à remarquer qu’au voisinage du maximum, pour une mole de tels systèmes, C ^S est de l’ordre de R /2 tandis que C ^R, C ^e, C ^M tendent vers zéro aux basses températures. Il arrive qu’une anomalie de Schottky augmente ainsi considérablement la chaleur spécifique: par exemple, des niveaux dont l’origine est le magnétisme nucléaire donnent à l’holmium une capacité calorifique par mole mille fois supérieure environ à celle du cuivre à 1 K.

De telles anomalies peuvent aussi provenir du magnétisme atomique; c’est le cas des sels magnétiques utilisés dans la désaimantation adiabatique. Le maximum de C ^S se produit à une température de l’ordre de /2k ; il n’est pas rare qu’il se trouve à des températures inférieures à 10^-2, voire 10^-4 K; ces phénomènes deviennent très importants à des températures aussi basses où il suffit de quelques impuretés pour les provoquer ^{[cf. CRISTAUX - Défauts dans les cristaux]}.

Propriétés magnétiques: loi de Curie

La plupart des propriétés magnétiques sont également étudiées aux températures plus élevées et ne relèvent pas spécifiquement de cet article, bien qu’elles constituent une part importante de l’activité des laboratoires de cryophysique. On ne parlera ici que du paramagnétisme, d’origine atomique ou nucléaire, qui joue un rôle privilégié à la fois pour l’obtention et la mesure des basses températures.

Soit un moment magnétique 猪 dans un champ H ; l’énergie vaut 漣 猪 H s’il est parallèle à H et de même sens, et + 猪 H s’il est de sens opposé. Supposons de plus que ces deux orientations du moment soient les seules possibles (cette hypothèse est d’ailleurs justifiée en mécanique quantique si le moment 猪 a un spin 1/2). On a alors deux niveaux d’énergie E ⁰ = 漣 猪 H et E ¹ = + 猪 H , dont la séparation E ¹ 漣 E ⁰ = 2 猪 H est proportionnelle au champ. Grâce au facteur de Boltzmann, le niveau fondamental est plus probable que le niveau excité: un plus grand nombre de moments sont dans le sens du champ, et la substance est aimantée. Pour de faibles valeurs de H , l’aimantation M est proportionnelle à H : M = 﨑 H ( 﨑 = susceptibilité magnétique). Une extension simple de (1) donne la loi de Curie:

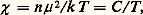où n est le nombre de moments contenus dans la substance. La susceptibilité est inversement proportionnelle à la température absolue et peut donc devenir très grande. C’est la seule grandeur physique simple qui ait un tel comportement, et c’est pour cela qu’on l’utilise pour définir l’échelle des températures au-dessous de 1 K. La loi de Curie n’est exacte que si les moments sont sans interaction entre eux; sinon elle devient:

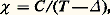pour T 礪 , où est caractéristique des forces d’interaction.

La loi de Curie est utilisée pour les mesures de températures en dessous de 1 K; jusque vers 10^-2 K, on utilise les propriétés du magnétisme atomique dans les sels magnétiques dilués, tels que, par exemple, le nitrate de cérium et de magnésium, Ce²Mg³(NO³)¹²24H²O; en dessous de 10^-2K, on aime mieux faire appel aux moments nucléaires dont les interactions sont plus faibles.

Résistance électrique

Un métal est caractérisé, au point de vue électrique, par sa résistivité 福 , qui intervient dans les lois d’Ohm et de Joule (transformation d’énergie électrique en chaleur). 福 décrit en quelque sorte le frottement des électrons entraînés par le champ électrique, à l’intérieur du cristal. Ce frottement résulte des collisions entre les électrons et les impuretés ou irrégularités de toutes sortes. Plus précisément, si 精 est le temps moyen entre deux collisions successives subies par un électron, on démontre que:

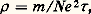où N est le nombre d’électrons, de charge e et de masse m , contenus dans l’unité de volume du cristal.

Les collisions sont de plusieurs types:

– avec les impuretés: 1/ 精 ⁱ est proportionnel au nombre de ces impuretés et ne varie pas avec la température;

– avec les irrégularités dues à l’agitation thermique ou avec ce que l’on a appelé plus haut les phonons: 1/ 精 ^p croît avec le nombre de phonons, donc avec la température; aux basses températures, 1/ 精 ^p varie en T ⁵ et, aux températures de l’ordre de la température de Debye, en T .

Lorsque plusieurs types de collisions ont lieu simultanément, les inverses des 精 correspondants (les probabilités de collision) s’ajoutent, et la résistivité totale est la somme des résistivités dues à chaque processus (règle de Matthiessen):

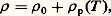où 福 ⁰ est la résistivité résiduelle due aux impuretés, 福 ^p(T ) la contribution des phonons variant au début en T ⁵, puis en T ^{[cf. CONDUCTION DE L'ÉLECTRICITÉ]}.

La résistivité résiduelle devient prépondérante à basses températures; elle est d’autant plus faible qu’il y a moins d’impuretés ou de défauts; on caractérise très souvent le degré de pureté ou de perfection d’un métal par le rapport de la résistivité résiduelle à sa résistivité à la température ambiante. Pour l’aluminium, on atteint assez facilement des rapports de résistivité de 福 (300 K)/ 福 ⁰ 礪 10³.

Conduction thermique

C’est un phénomène très semblable à la conduction électrique: si on applique une différence de température T aux extrémités d’un cylindre de longueur l et de section s , il laisse passer par seconde une quantité de chaleur Q telle que:

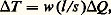selon la loi de Fourier ^{[cf. THERMODYNAMIQUE]}, où w , résistivité thermique, est caractéristique de l’échantillon. On définit de même la conductivité thermique = 1/w .

Isolants électriques

Ils ne possèdent pas d’électrons de conduction, et la chaleur est transportée par les seules excitations existantes, les phonons, quanta d’énergie d’agitation thermique des atomes, qui se propagent dans le cristal avec la vitesse v du son.

On utilise une formule établie en théorie cinétique des gaz:

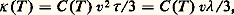où C (T ) est la chaleur spécifique du gaz de phonons, est le libre parcours moyen des phonons: distance moyenne parcourue entre deux chocs successifs séparés par l’intervalle de temps 精 ; 精 et = v 精 varient avec la température et la nature de l’échantillon.

Aux très basses températures, les valeurs de sont très élevées. Pour un bon monocristal, n’est limité que par les diffusions sur les parois latérales du cylindre. Par suite, = d (d = diamètre du cylindre) et, comme C varie en T ³ (cf. supra ), 黎 T ³d .

Il est tout à fait remarquable que puisse ainsi, dans certains cas, dépendre du diamètre de l’échantillon. Cet effet (effet Casimir) est très bien observé. Pour un polycristal, d est de l’ordre de la dimension moyenne des cristallites.

Aux températures élevées, C ne suit plus la loi en T ³, mais tend vers 3 R (Dulong et Petit). Les phonons sont très nombreux, leur nombre varie comme T et les collisions des phonons entre eux deviennent prédominantes; par suite, 黎 1/T et 黎 1/T sont des fonctions décroissantes de T .

Aux températures intermédiaires, passe par un maximum obtenu souvent pour des températures de l’ordre de /10. Au voisinage de ce maximum, est très sensible aux impuretés ou irrégularités de structure. Pour des isolants électriques très purs, la valeur maximale de est souvent très élevée et bien supérieure à celle des métaux comme le cuivre, pourtant considérés comme bons conducteurs de la chaleur (fig. 3).

Métaux

Comme les phonons, les électrons peuvent participer au transport de chaleur; leur contribution est même en général la plus importante, car les phonons ont un libre parcours moyen fortement diminué par leurs collisions avec les électrons. On démontre que, dans un cas idéal, pour les conductivités d’origine électronique, il y a une relation (Wiedemann-Franz) entre la conductivité électrique 靖 et la conductivité thermique :

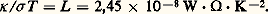La loi de Wiedemann-Franz est bien vérifiée aux basses et hautes températures, mais pas aux températures intermédiaires. Ce qui a été dit de la résistivité électrique 福 = 靖 ^-1 permet de prévoir les variations de (T ). Aux basses températures, 靖 = 靖 ⁰ (conductivité résiduelle) et = L 靖 ⁰T varie comme T et donc tend vers zéro à 0 K. Aux températures plus élevées, 靖 黎 1/T , et la conductibilité thermique devient constante. Entre ce palier et la région linéaire des basses températures, on observe un maximum. Signalons ici que pour un corps à l’état supraconducteur, la relation de Wiedemann-Franz n’est plus valable et la conductivité thermique, d’origine électronique, est fortement abaissée. Il reste alors essentiellement la contribution des phonons, et est plus petit que pour un métal normal. On réalise sur ce principe des interrupteurs thermiques, en utilisant des fils supraconducteurs. L’application d’un champ magnétique suffisant détruit la supraconductivité, et augmente considérablement; des variations de de l’ordre de 100 sont tout à fait usuelles.

Superfluidité et supraconductivité

Certaines des propriétés physiques présentent une variation régulière avec la température, d’autres au contraire sont spécifiques des très basses températures. C’est le cas de la superfluidité ou de la supraconductivité.

Le premier phénomène est la disparition complète de viscosité dans l’écoulement de l’hélium, à faible vitesse, en dessous d’une certaine température critique. Le second phénomène est l’extraordinaire propriété de certains métaux ou alliages qui, en dessous de leur champ magnétique critique, ont une résistivité électrique rigoureusement nulle.

Étant donné l’importance de ces phénomènes et l’abondance croissante de leurs applications à l’échelle industrielle, un article détaillé est consacré séparément à chacun d’eux (cf. SUPERFLUIDITÉ et SUPRACONDUCTIVITÉ).

2. Méthodes de réfrigération à basse température

Le principe général de réfrigération, quel que soit le système, consiste, à température constante, à augmenter l’état d’ordre, donc à diminuer l’entropie, par variation d’un paramètre physique, pression, champ magnétique, etc., puis, après avoir isolé thermiquement le système, à ramener le paramètre physique à sa valeur initiale de manière adiabatique. Ce principe est utilisé pour la désaimantation adiabatique ainsi que, sous diverses formes, pour la liquéfaction des gaz.

Les différents domaines

La cryophysique fait appel, de manière plus ou moins directe, à l’utilisation de gaz liquéfiés; on peut ainsi définir plusieurs domaines suivant les fluides utilisés. On en distingue trois: ceux de l’air, de l’hydrogène et de l’hélium liquides. À l’intérieur de chacun de ces domaines, on fait varier la température d’une manière continue en modifiant la pression au-dessus du liquide depuis le point critique jusqu’au point triple (sauf pour l’hélium qui reste liquide sous sa pression de vapeur saturante jusqu’à 0 K).

Notons également que les chaleurs latentes de vaporisation sont différentes et qu’à volume égal la puissance frigorifique de l’hélium est inférieure d’un facteur 10 à celle de l’hydrogène, d’un facteur 100 à celle de l’azote et d’un facteur 1 000 à celle de l’eau (tabl. 3).

Approche du zéro absolu

En pratique, la faible tension de vapeur de l’hélium ordinaire (constitué essentiellement de l’isotope 4) ne permet pas de descendre en dessous de 0,7 K. L’isotope 3 de l’hélium, obtenu comme sous-produit de la préparation des matériaux pour la fusion thermonucléaire, a permis de notables progrès. Les deux isotopes, obéissant à des statistiques différentes (Bose-Einstein pour le ⁴He et Fermi-Dirac pour le ³He), ont des comportements très différents; en particulier, l’hélium 3 a une tension de vapeur très supérieure à celle de l’hélium 4 (10⁴ fois plus grande à 0,5 K). Grâce à cette propriété, en pompant le gaz au-dessus du liquide, on arrive dans des conditions raisonnables à descendre jusque vers 0,21 K.

Pour les températures inférieures, on utilise la désaimantation adiabatique ou la dilution de l’isotope 3 de l’hélium dans l’isotope 4.

Une place à part doit être réservée au refroidissement optique d’une vapeur comme le césium ou d’un gaz comme l’hélium, en ce sens que seule l’agitation du gaz tend vers zéro, et que le système ne peut pas servir de réfrigérateur. On dispose pour cela de lasers de fréquence 益 ^L très légèrement inférieure à une fréquence d’absorption optique de la vapeur: 益 ^a. Si un atome se rapproche du laser, l’effet Doppler fait croître 益 ^L et augmente la section efficace d’absorption 靖 (fig. 4). L’atome excité retourne dans son état fondamental par émission spontanée dans une direction aléatoire. La quantité de mouvement est donc transférée en moyenne à l’atome à chaque absorption, dans le sens d’un freinage. L’utilisation de six lasers opposés deux à deux suivant les trois axes permet de freiner toutes les composantes de la vitesse. Des températures de l’ordre de quelques microkelvins ont ainsi été atteintes.

Désaimantation adiabatique

Reprenons l’exemple du paragraphe sur les propriétés magnétiques où l’on a placé des moments 猪 dans un champ H . À l’équilibre thermique, le rapport des probabilités des niveaux E ⁰ et E ¹ est e ⁺² size=1^{猪 H /kT} . Diminuons le champ H jusqu’à une valeur H 麗 H , mais en ayant soin d’isoler les moments magnétiques de tout contact thermique avec le milieu extérieur (en faisant par exemple le vide autour de l’échantillon). On effectue ainsi ce qu’on appelle en thermodynamique une transformation adiabatique . Dans ces conditions, les probabilités des niveaux sont conservées et leur rapport garde la valeur e 2 猪 H /kT alors que le champ est devenu H . Or, dans le cas du champ H , ce rapport vaut e 2 猪 H /kT où T est la nouvelle température du corps. On a évidemment H /T = H /T ou T = T H /H : au cours de la désaimantation adiabatique, le système des moments magnétiques s’est refroidi. On dispose là d’une technique très puissante pour atteindre des températures inférieures à 1 K. Il semblerait qu’avec H = 0 on puisse atteindre T = 0 K; cependant, les formules précédentes ne sont plus valables lorsqu’on tient compte des interactions inévitables entre les moments, et, dans la pratique, T ne peut descendre en dessous d’une certaine valeur dépendant de la substance.

Avec des substances ayant des moments magnétiques électroniques, on peut descendre jusque vers 10^-2 K. Pour des substances portant des moments nucléaires, il est possible de descendre beaucoup plus bas. Des températures de spin de 10^-6 K ont été atteintes, mais il se pose pour ces températures extrêmes des problèmes très sérieux, liés, en particulier, au contact thermique entre les noyaux et le réseau. La désaimantation est une méthode très puissante, mais elle a des inconvénients: elle ne permet pas une production continue de froid, elle prohibe pratiquement les mesures sous un champ magnétique (qui ramènerait le système à sa température initiale).

Dilution de l’isotope 3 de l’hélium dans l’isotope 4

Un procédé découvert vers 1960 permet un fonctionnement continu sans champ magnétique. C’est le réfrigérateur à dilution d’hélium 3 dans l’hélium 4 qui avait été proposé par London et Mendoza [cf. CRYOLOGIE Cryogénie (Les réfrigérateurs à dilution)]. Le principe consiste à enlever des calories en évaporant un liquide. Le liquide est de l’hélium 3 pratiquement pur; le rôle de la vapeur est joué par de l’hélium 3 en solution dans de l’hélium 4 liquide.

3. Applications de la cryophysique

Domaine de l’hydrogène liquide

La séparation des constituants d’un mélange gazeux par distillation à basse température est devenue l’une des techniques les plus rentables; ainsi, c’est dans sa distillation en vue de séparer les quelque 10 millièmes de deutérium qu’il contient que l’hydrogène liquide a trouvé sa première application massive. Le deutérium ainsi séparé, d’ailleurs sous forme de HD, sert à la fabrication de l’eau lourde, utilisée en physique nucléaire. Celle-ci a fait appel à l’hydrogène liquide pour les chambres à bulles, qui atteignent actuellement des dizaines de mètres cubes de volume utile. Leur intérêt est de présenter un milieu simple de densité élevée en protons. C’est dans le domaine spatial que l’hydrogène liquide est le plus employé. Étant le plus léger de tous les fluides, l’hydrogène est incomparable en matière de propulsion de fusées, où il donne les impulsions spécifiques les plus élevées.

La production en très grande quantité d’hydrogène liquide a abaissé son prix de revient, qui est actuellement au litre de l’ordre de grandeur de celui de l’essence, tout au moins aux États-Unis. Cette diminution de prix permet d’envisager de nouvelles utilisations de l’hydrogène liquide; par exemple comme carburant dans les avions à réaction ou dans les piles électriques à combustible.

L’hydrogène liquide, bien que manipulé communément, nécessite quelques précautions en présence de l’oxygène atmosphérique. Pour le stockage de longue durée, il faut également s’assurer à l’aide de catalyseurs qu’il est liquéfié sous la forme «parahydrogène» (sinon la forme «ortho» se transforme en «para» avec dégagement de chaleur).

Domaine de l’hélium liquide

La propriété fondamentale utilisable, dans ce domaine de température, est la supraconductivité. Malgré la découverte des supraconducteurs à haute température critique (T ^c de l’ordre de 100 K), ceux-ci sont fragiles, donc difficiles à mettre en forme, et ne portent que des courants relativement faibles à 77 K. Ce n’est que vers 1960 que sont apparus des alliages restant supraconducteurs dans un champ magnétique élevé: alliage de niobium-zirconium (7 teslas) puis le niobium-étain (20 teslas) et le niobium-titane (12 teslas). Ces alliages ont permis la réalisation de bobinages pour créer des champs magnétiques intenses continus dans des volumes de plus en plus grands. Pour améliorer leur stabilité, les fils ou rubans supraconducteurs sont enrobés de métal normal, bon conducteur de la chaleur et de l’électricité comme le cuivre ou l’aluminium. Pour les futures grandes chambres à bulles, on construit des bobines supraconductrices, qui créent des champs d’induction magnétique de plusieurs teslas dans des volumes de plusieurs mètres cubes.

Le confinement magnétique des plasmas des tokamaks est grandement amélioré par l’utilisation de supraconducteurs, car l’induction magnétique est beaucoup plus élevée qu’en solution classique, est surtout gratuite en énergie par absence d’effet Joule dans les bobinages du champ toroïdal. La présence d’un champ poloïdal variable engendre des pertes, bien évacuées par l’utilisation d’hélium superfluide (T 麗 2,17 K) [cf. SUPERFLUIDITÉ], ce qui est le principe du tokamak Tore-2 Supra à Cadarache. La conjonction des très basses températures et de la microlithographie a ouvert, en 1989, la possibilité d’une électronique à un seul électron. Si on considère un tronçon métallique relié par deux jonctions tunnel (J) [cf. mécanique QUANTIQUE], des électrons peuvent sauter dans le tronçon (fig. 5). La capacité C se charge alors, et l’énergie mise en jeu est:

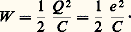Tant que kT 礪 W , le nombre d’électrons fluctue dans le tronçon (analogie avec le bruit Nyquist). Dans le cas inverse, seul un potentiel V = e /C appliqué à la ligne est capable d’ajouter un électron. Pour des dimensions micrométriques, T doit être inférieur ou égal à 1 K.

Il faut enfin noter que, dans ce domaine de températures, les masers et de nombreux détecteurs de rayonnement infrarouge fonctionnent avec une sensibilité considérablement augmentée par la diminution importante du bruit de fond d’origine thermique.

L’hélium liquide, en dessous de 2,17 K, devient superfluide ^{[cf. SUPERFLUIDITÉ]}.

4. Mesure des températures

Jusqu’à la température de l’oxygène liquide, la thermométrie est classique, et on peut utiliser aussi bien un thermomètre à liquide (pentane) qu’un thermomètre à résistance de platine ou un thermocouple. La définition de l’échelle de températures jusqu’à environ 1 K se fait au moyen du classique thermomètre à gaz à hélium.

Pression de vapeur saturante

La mesure de la pression de vapeur des différents liquides cryogéniques constitue la base la plus pratique de repérage des températures et c’est en général à elle que l’on se réfère pour étalonner les thermomètres d’interpolation. Avec l’hélium 4, les phénomènes de superfluidité peuvent fausser la mesure de la pression dans un bulbe à cause du film qui grimpe le long des parois, se vaporise dans le capillaire et vient se recondenser dans le bulbe. Ces inconvénients sont supprimés par l’emploi de l’hélium 3 de 0,3 à 3 K.

Thermomètre à résistance

Le thermomètre à résistance de platine peut être utilisé encore vers 10 K, mais ne suit plus la loi simple de variation. Dans le domaine de la cryophysique, ce sont plutôt les thermomètres à semi-conducteurs qui semblent donner la meilleure sensibilité et la meilleure reproductibilité de 1 à 100 K. Certaines résistances radio du commerce ont, comme les semi-conducteurs, un coefficient de température négatif et peuvent être utilisées jusqu’à quelques centièmes de degré absolu. Ces thermomètres ont cependant une mauvaise conductibilité thermique, et il est nécessaire d’utiliser de très faibles puissances électriques pour la mesure de la résistance.

Couples thermoélectriques

Les couples thermoélectriques de métaux usuels ont une sensibilité qui décroît avec la température, et le classique couple cuivre-constantan ne peut guère être utilisé en dessous de la température de l’hydrogène liquide. Les couples à alliages dilués or-cobalt d’abord puis or-fer ont permis d’étendre la gamme de mesure jusqu’à 1 K et sont très précieux pour les mesures différentielles de température.

Thermomètre pour T size=5麗 1 K

En dessous de 1 K, la mesure des susceptibilités d’un sel paramagnétique fournit une thermométrie absolue, grâce à la loi de Curie, 﨑 = C /T , à condition d’être étalonné dans une zone de températures connue au-dessus de 1 K. Le thermomètre à nitrate de cérium et de magnésium permet une bonne définition de la température jusque vers 5 憐 10^-3 K. Pour les températures plus basses, il faut faire appel au magnétisme nucléaire, mais alors se pose le problème de la définition même de la température du système. Toutes les mesures de températures au-dessous de 1 K sont rendues délicates par la difficulté d’établir l’équilibre thermique. Cette difficulté est accrue avec les sels paramagnétiques du fait de leur mauvaise conductibilité thermique. Une méthode élégante consiste à utiliser une mesure de la susceptibilité nucléaire d’un métal; la mesure statique ne peut être faite qu’aux températures extrêmement basses, alors qu’une mesure dynamique par résonance magnétique nucléaire pulsée permet d’étendre le domaine de mesure jusque vers 1 kelvin.

Encyclopédie Universelle. 2012.